Efecto Seebeck
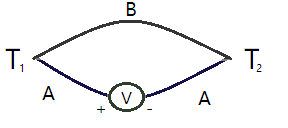
El efecto Seebeck es la conversión de diferencias de temperatura directamente a electricidad
fem = αAB · ΔT = (αA - αB) · ΔT
|
fem = fuerza electromotriz (µV)
αA, αB = potencias termoeléctricas absolutas de los metales
αAB = coeficiente de seebeck (µV/K)
ΔT = diferencia de temperatura (K)(T1 - T2)
|
| Material |
Coeficiente de Seebeck
(µV/K) |
|
Selenio
|
900
|
|
Silicio
|
440
|
|
Germanio
|
330
|
|
Antimonio
|
47
|
|
Cadmio, Tungsteno
|
7.5
|
|
Oro, Plata, Cobre
|
6.5
|
|
Rodio
|
6
|
|
Tántalo
|
4.5
|
|
Plomo
|
4
|
|
Aluminio
|
3.5
|
|
Carbón
|
3
|
|
Mercurio
|
0.6
|
|
Platino
|
0
|
|
Sodio
|
-2
|
|
Potasio
|
-9
|
|
Níquel
|
-15
|
|
Constantan
|
-35
|
| Bismuto |
-72 |
| Aluminio (Al) |
+1,5 a +2,0 |
| Cobre (Cu) |
+1,5 a +2,0 |
| Oro (Au) |
+1,5 a +2,5 |
| Plata (Ag) |
+1,5 a +2,0 |
| Hierro (Fe) |
+5,5 a +6,0 |
| Níquel (Ni) |
-15,5 a -30,0 |
| Constantán (CuNi) |
-35,5 a -45,0 |
Efecto Peltier
Hace referencia a la creación de una diferencia de temperatura a un partir de una diferencia de potencial eléctrico
|
Q = ПAB · I = (ПB - ПA) · I
|
Q = el calor Peltier absorbido por la unión inferior por unidad de tiempo
ПAB = coeficiente Peltier
ПA, ПB = coeficientes de cada material
I = intensidad de corriente
|
Efecto Thomson
| q = µ · I · ΔT |
µ = coeficiente de Thomson
I = intensidad de corriente
q = absorción o liberación de calor
|
Arrastre de fotones
|
T ≈ 1 / 5 · θD
|
θD = Temperatura de Debye
|
| Material | temperaturas de Debye |
|---|
| Aluminio |
428 K |
| Cadmio | 209 K |
| Cromo | 630 K |
| Oro | 165 K |
| Hierro | 470 K |
| Plomo | 105 K |
| Manganeso | 410 K |
| Níquel | 450 K |
| Platino | 240 K |
| Silicio | 645 K |
| Plata |
225 K |
| Tántalo | 240 K |
| Estaño (blanco) | 200 K |
| Titanio | 420 K |
| Wolframio | 400 K |
| Zinc | 327 K |
| Carbono | 2230 K |
| Hielo | 192 K |
Conductividad térmica de los electrones
| Ke = (1/3) · CVe · v · l |
v = velocidad de los electrones
l = trayectoria libre media
CVe = capacidad calorífica de una unidad de volumen, debido a electrones |