Variación de la fase al pasar por una reactancia
Cuando una señal eléctrica atraviesa una reactancia en un circuito, se produce una variación en su fase dependiendo de la frecuencia y la relación entre reactancia y resistencia. En un inductor, la corriente se retrasa respecto al voltaje debido a la acumulación de energía en el campo magnético, mientras que en un capacitor, la corriente se adelanta porque el campo eléctrico modula el flujo de carga. La magnitud de esta variación se expresa mediante el ángulo de fase θ , que depende de la reactancia X y la resistencia R del circuito. Comprender este efecto es crucial en el diseño de filtros, redes de adaptación y sistemas de transmisión de señales.
|
Fórmula de cálculo:
θ = arctan(X / R)
Fórmula derivada:
dθ / dX = 1 / (1 + ( X / R )² )
|
θ = Ángulo de fase en radianes
X = Reactancia, en Henrios o Faradios
R = Resistencia eléctrica (Ohmios)
ω = Pulsación en radianes por segundo (rad/s), definida como ( ω = 2 · π · f )
δ = Factor de amortiguamiento
ƞ = Eficacia del filtro, indicador del pico de resonancia
α = Coeficiente de filtrado, relacionado con la atenuación
Δω = Ancho de banda en pulsación, diferencia entre dos frecuencias angulares ( Δω = ω2 - ω1 )
ωr = Frecuencia angular de resonancia, definida como ωr = 1 / √( L · C )
L = Inductancia en Henrios (H)
C = Capacitancia en Faradios (F)
f = Frecuencia en Hertz (Hz)
XL = Reactancia inductiva ( XL = ω · L )
XC = Reactancia capacitiva ( XC = 1 / (ω · C) )
dX = Diferencial de la reactancia, indica pequeños cambios en **X** con respecto a otra variable
dω = Diferencial de la pulsación, representa una pequeña variación en **ω**
A representa la atenuación en decibeles (dB)
|
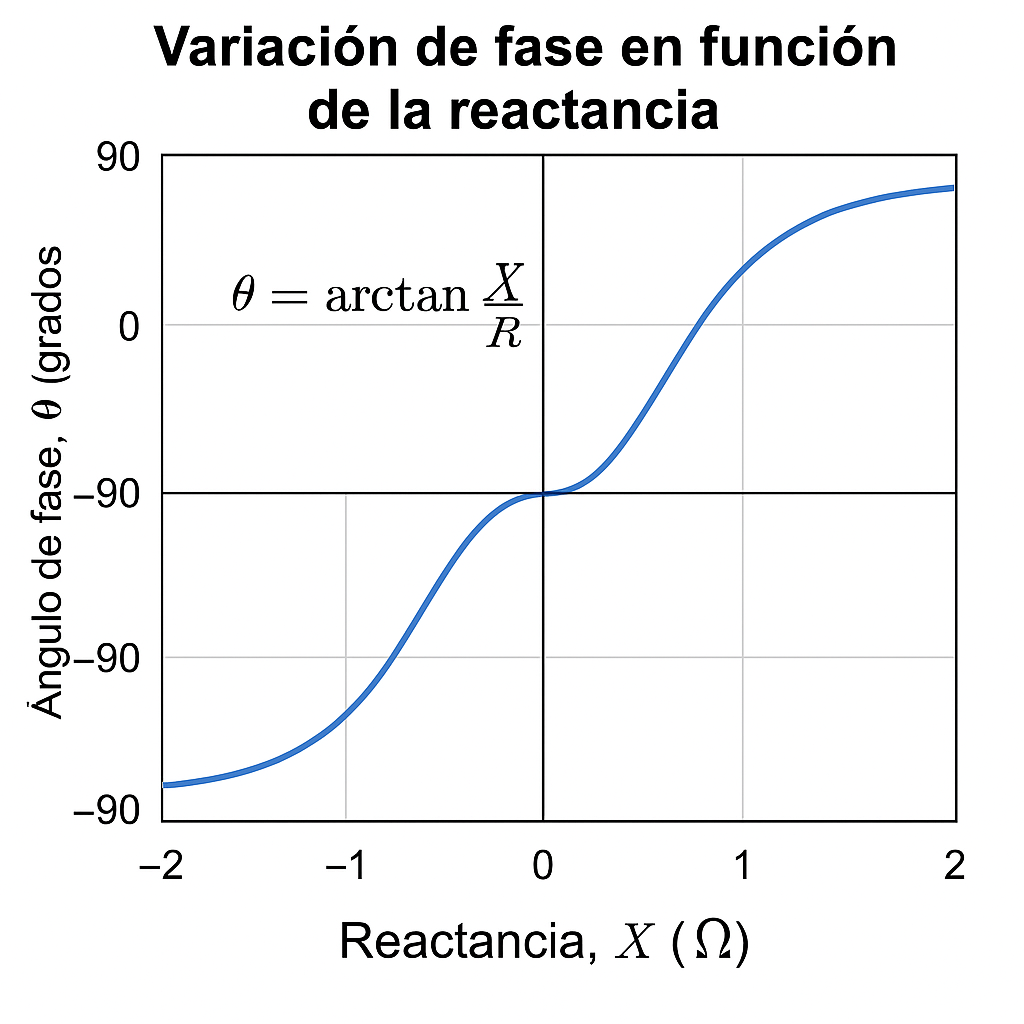Ejemplo de cálculo:
Si R = 50Ω y X = 100Ω, entonces:
θ = arctan(100 / 50) = arctan(2) ≈ 63.43°
Solución:
La fase varía aproximadamente 63.43° al pasar por esta reactancia.
Fórmulas adicionales sobre la variación de fase
|
Relación entre fase y frecuencia angular (ω)
La reactancia está vinculada con la frecuencia angular:
Para **inductores**: ( XL = ω · L )
Para **capacitores**: ( XC = 1 / (ω · C) )
Variación de fase:
θ = arctan(ω · L / R) (para un inductor)
θ = arctan(1 / (ω · C · R)) (para un capacitor)
|
|
Derivada de la fase respecto a ω
dθ/dω = R / (R² + X²) · dX/dω
Esta ecuación muestra cómo la variación de la fase depende del cambio de reactancia respecto a la frecuencia angular.
|
|
Eficacia del filtro (ƞ) y su efecto en la fase
ƞ = ωr / Δω
A mayor ƞ, más pronunciada será la variación de fase cerca de la frecuencia de resonancia.
|
|
Coeficiente de filtrado (α) y atenuación
A = 20 log(1 / α)
Cuando α es grande, el filtro atenúa menos, lo que permite una variación de fase más marcada.
|